How far did I go?

Back in the day we read guidebooks, and those told us how long a hike was.

We also used maps, and would estimate distances using a ruler, and a scale.

The modern way is to carry a GPS, and trust it to measure the distance travelled. Which brings us to a very modern, and sometimes difficult to explain phenomenon.

The distance measured on a GPS is almost always going to be further than the previous ways of measuring distances.

The Coastline Paradox

The reason for the discrepancy has to do with the mathematics of fractals, a little bit of calculus, and something called the Coastline Paradox.

We can compare a hiking route to the coastline of a country, or the path of a river, or perhaps even a trail or a road. The basic concept is that things like this do not have a very well defined length.

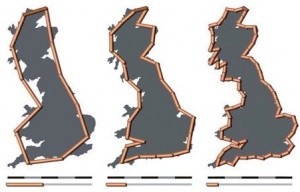
Basically, the length of the coastline, river or trail depends on the size of the ruler you use to measure it.

The sum of several straight lines approximating a curved path will always be less than the actual length of the path. Using segments that are smaller in length will result in a slightly longer length. The smaller the line segment used to appoximate the curve, the longer the path, and the closer the approximation to the actual length. Using calculus, we can make the line lengths arbitrarily small, and calculate the length of a curve.

Note that this does not mean that the length keeps getting bigger forever. This means the distance approaches a limit, which is the actual length of the curved path.

Canadians should feel proud that our coastline, by any ruler, is the longest.

Maps and Measurement

To translate this to the real word, if you use a large ruler, for instance a map where 1 cm=1000 m (1:100,000), then the smallest unit of measurement is probably 0.5 cm or 500 m. You’ll get a measurement of the path on the order of 500 m in length. If you choose a map with a larger scale, you’ll usually get a slightly larger number.

Now we switch to a GPS. Depending on your device, and the settings, it may be set to record your track every few seconds, or minutes (time based), or every few metres (distance based). The scale of this measurement is almost always more accurate than the scale at which a map, or guidebook is drawn – sometimes on the order of 5-10 m.

You are using a smaller ruler!

Of course this always leads to arguments between the guidebook writer, race directors, and particularly competitive individuals (I’m looking at the Strava enthusiasts here) who make it an important part of their lives to compare these distances.

There’s a simiar effect for elevation gain and drop. While a mountain has a definite point measurement elevation, the path to the top of a mountain is a “curve” which has a total elevation gain and drop (length) that depends on the size of the ruler measuring it.

Solutions?

How do we answer the question, “How far did I go?”

As GPS units get better, it is possible that guidebooks and race directors will start updating the distances and elevations on their trails. There will always be some discrepancy, but I expect that the differences in measurement will start converging, and most of these arguments will go away. By the time the GPS can measure an individual’s step length, I figure people may stop caring about the discrepancy.

I think the important take-home is that all measurements are estimates, maps are representations of the real world, and even GPS units are just estimates of your location that, while accurate, contain a certain amount of uncertainty.