Measuring GPS Precision
Two years ago I wrote a post on how to measure your own GPS accuracy, and followed that up with a post on measuring the accuracy of a smartphone GPS. This was in a series of posts on GPS units and various ways they lie to you on their accuracy, and how to better interpret what they are telling you.
Clarifications
First I’d like to clarify that I was using some pretty sloppy terminology.
Accuracy is used to indicate how close a measurement is to the true position.
Precision is used to talk about what the range, or error, in measurement is.
What we are talking about in the above two articles is precision, or a measurement of the size of the error, as expressed by a confidence interval.
There are a number of factors that contribute to error in a GPS position, most of which are beyond the control of an individual. Added to that are a few things that are inherent to a device, such as an external antenna, and the sophistication of the software. I believe that it is important for backcountry professionals to understand where the limits of measurement by GPS are, and to give them the tools to evaluate, compare, and visualize the precision of their tools.
So I took some of the tools I used to write my series of articles on GPS precision, and made a web site where people can test their own devices.
Methodology
The methodology of the web site is the same as that used in my posts from 2012.
- Record a GPS track while the device is stationary. I used about an hour as a good measure.
Make sure the device is turned on, and has time to develop a stable “lock” on the satellites in view.
Put it in one place, make sure it is recording positions regardless of whether the device is moving, and let it go. - Upload the track to the web site.
- The web site takes the positions and converts them to Transverse Mercator projection.
- It finds the “average” position, and uses that to normalize the data set as a set of offsets from that new axis.
- We calculate the following:
- standard deviation: $latex \sigma=\sqrt{\frac{1}{N}\sum_{i=1}^N(x_i-\mu)^2}$
- CEP $latex CEP=0.59(\sigma_x+\sigma_y)$
- 2DRMS: $latex 2DRMS=2\sqrt{\sigma_x^2+\sigma_y^2}$
- We create a scatter plot of the result
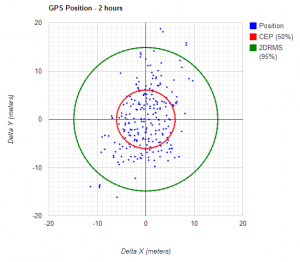
Community Effort
Feel free to create as many tests as you like for as many devices as you have. I’ll update the site to allow comparisons between devices using charts scaled the same if people are interested. Report all bugs to me. Feel free to comment below if you think this can be improved.
Interesting idea. I’ll have to see if I can record some data with my smart phones, especially the two that have GLONASS support.